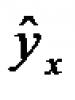≡× МЕНЮ

• Грамматика
• География
• СМИ
• Моя жизнь
• Книги

Аппроксимация функции методом наименьших квадратов. Математика на пальцах: методы наименьших квадратов Аппроксимация экспериментальных данных методом наименьших квадратов

Метод наименьших квадратов (МНК, англ. Ordinary Least Squares, OLS ) - математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов отклонений некоторых функций от искомых переменных. Он может использоваться для «решения» переопределенных систем уравнений (когда количество уравнений превышает количество неизвестных), для поиска решения в случае обычных (не переопределенных) нелинейных систем уравнений, для аппроксимации точечных значений некоторой функции. МНК является одним из базовых методов регрессионного анализа для оценки неизвестных параметров регрессионных моделей по выборочным данным.

Энциклопедичный YouTube

1 / 5

✪ Метод наименьших квадратов. Тема

✪ Метод наименьших квадратов, урок 1/2. Линейная функция

✪ Эконометрика. Лекция 5 .Метод наименьших квадратов

✪ Митин И. В. - Обработка результатов физ. эксперимента - Метод наименьших квадратов (Лекция 4)

✪ Эконометрика: Суть метода наименьших квадратов #2

Субтитры

История

До начала XIX в. учёные не имели определённых правил для решения системы уравнений , в которой число неизвестных меньше, чем число уравнений; до этого времени употреблялись частные приёмы, зависевшие от вида уравнений и от остроумия вычислителей, и потому разные вычислители, исходя из тех же данных наблюдений, приходили к различным выводам. Гауссу (1795) принадлежит первое применение метода, а Лежандр (1805) независимо открыл и опубликовал его под современным названием (фр. Méthode des moindres quarrés ) . Лаплас связал метод с теорией вероятностей , а американский математик Эдрейн (1808) рассмотрел его теоретико-вероятностные приложения . Метод распространён и усовершенствован дальнейшими изысканиями Энке , Бесселя , Ганзена и других.

Сущность метода наименьших квадратов

Пусть x {\displaystyle x} - набор n {\displaystyle n} неизвестных переменных (параметров), f i (x) {\displaystyle f_{i}(x)} , , m > n {\displaystyle m>n} - совокупность функций от этого набора переменных. Задача заключается в подборе таких значений x {\displaystyle x} , чтобы значения этих функций были максимально близки к некоторым значениям y i {\displaystyle y_{i}} . По существу речь идет о «решении» переопределенной системы уравнений f i (x) = y i {\displaystyle f_{i}(x)=y_{i}} , i = 1 , … , m {\displaystyle i=1,\ldots ,m} в указанном смысле максимальной близости левой и правой частей системы. Сущность МНК заключается в выборе в качестве «меры близости» суммы квадратов отклонений левых и правых частей | f i (x) − y i | {\displaystyle |f_{i}(x)-y_{i}|} . Таким образом, сущность МНК может быть выражена следующим образом:

∑ i e i 2 = ∑ i (y i − f i (x)) 2 → min x {\displaystyle \sum _{i}e_{i}^{2}=\sum _{i}(y_{i}-f_{i}(x))^{2}\rightarrow \min _{x}} .

В случае, если система уравнений имеет решение, то минимум суммы квадратов будет равен нулю и могут быть найдены точные решения системы уравнений аналитически или, например, различными численными методами оптимизации. Если система переопределена, то есть, говоря нестрого, количество независимых уравнений больше количества искомых переменных, то система не имеет точного решения и метод наименьших квадратов позволяет найти некоторый «оптимальный» вектор x {\displaystyle x} в смысле максимальной близости векторов y {\displaystyle y} и f (x) {\displaystyle f(x)} или максимальной близости вектора отклонений e {\displaystyle e} к нулю (близость понимается в смысле евклидова расстояния).

Пример - система линейных уравнений

В частности, метод наименьших квадратов может использоваться для «решения» системы линейных уравнений

A x = b {\displaystyle Ax=b} ,

где A {\displaystyle A} прямоугольная матрица размера m × n , m > n {\displaystyle m\times n,m>n} (т.е. число строк матрицы A больше количества искомых переменных).

Такая система уравнений в общем случае не имеет решения. Поэтому эту систему можно «решить» только в смысле выбора такого вектора x {\displaystyle x} , чтобы минимизировать «расстояние» между векторами A x {\displaystyle Ax} и b {\displaystyle b} . Для этого можно применить критерий минимизации суммы квадратов разностей левой и правой частей уравнений системы, то есть (A x − b) T (A x − b) → min x {\displaystyle (Ax-b)^{T}(Ax-b)\rightarrow \min _{x}} . Нетрудно показать, что решение этой задачи минимизации приводит к решению следующей системы уравнений

A T A x = A T b ⇒ x = (A T A) − 1 A T b {\displaystyle A^{T}Ax=A^{T}b\Rightarrow x=(A^{T}A)^{-1}A^{T}b} .

МНК в регрессионном анализе (аппроксимация данных)

Пусть имеется n {\displaystyle n} значений некоторой переменной y {\displaystyle y} (это могут быть результаты наблюдений, экспериментов и т. д.) и соответствующих переменных x {\displaystyle x} . Задача заключается в том, чтобы взаимосвязь между y {\displaystyle y} и x {\displaystyle x} аппроксимировать некоторой функцией , известной с точностью до некоторых неизвестных параметров b {\displaystyle b} , то есть фактически найти наилучшие значения параметров b {\displaystyle b} , максимально приближающие значения f (x , b) {\displaystyle f(x,b)} к фактическим значениям y {\displaystyle y} . Фактически это сводится к случаю «решения» переопределенной системы уравнений относительно b {\displaystyle b} :

F (x t , b) = y t , t = 1 , … , n {\displaystyle f(x_{t},b)=y_{t},t=1,\ldots ,n} .

В регрессионном анализе и в частности в эконометрике используются вероятностные модели зависимости между переменными

Y t = f (x t , b) + ε t {\displaystyle y_{t}=f(x_{t},b)+\varepsilon _{t}} ,

где ε t {\displaystyle \varepsilon _{t}} - так называемые случайные ошибки модели.

Соответственно, отклонения наблюдаемых значений y {\displaystyle y} от модельных f (x , b) {\displaystyle f(x,b)} предполагается уже в самой модели. Сущность МНК (обычного, классического) заключается в том, чтобы найти такие параметры b {\displaystyle b} , при которых сумма квадратов отклонений (ошибок, для регрессионных моделей их часто называют остатками регрессии) e t {\displaystyle e_{t}} будет минимальной:

b ^ O L S = arg ⁡ min b R S S (b) {\displaystyle {\hat {b}}_{OLS}=\arg \min _{b}RSS(b)} ,

где R S S {\displaystyle RSS} - англ. Residual Sum of Squares определяется как:

R S S (b) = e T e = ∑ t = 1 n e t 2 = ∑ t = 1 n (y t − f (x t , b)) 2 {\displaystyle RSS(b)=e^{T}e=\sum _{t=1}^{n}e_{t}^{2}=\sum _{t=1}^{n}(y_{t}-f(x_{t},b))^{2}} .

В общем случае решение этой задачи может осуществляться численными методами оптимизации (минимизации). В этом случае говорят о нелинейном МНК (NLS или NLLS - англ. Non-Linear Least Squares ). Во многих случаях можно получить аналитическое решение. Для решения задачи минимизации необходимо найти стационарные точки функции R S S (b) {\displaystyle RSS(b)} , продифференцировав её по неизвестным параметрам b {\displaystyle b} , приравняв производные к нулю и решив полученную систему уравнений:

∑ t = 1 n (y t − f (x t , b)) ∂ f (x t , b) ∂ b = 0 {\displaystyle \sum _{t=1}^{n}(y_{t}-f(x_{t},b)){\frac {\partial f(x_{t},b)}{\partial b}}=0} .

МНК в случае линейной регрессии

Пусть регрессионная зависимость является линейной:

y t = ∑ j = 1 k b j x t j + ε = x t T b + ε t {\displaystyle y_{t}=\sum _{j=1}^{k}b_{j}x_{tj}+\varepsilon =x_{t}^{T}b+\varepsilon _{t}} .

Пусть y - вектор-столбец наблюдений объясняемой переменной, а X {\displaystyle X} - это (n × k) {\displaystyle ({n\times k})} -матрица наблюдений факторов (строки матрицы - векторы значений факторов в данном наблюдении, по столбцам - вектор значений данного фактора во всех наблюдениях). Матричное представление линейной модели имеет вид:

y = X b + ε {\displaystyle y=Xb+\varepsilon } .

Тогда вектор оценок объясняемой переменной и вектор остатков регрессии будут равны

y ^ = X b , e = y − y ^ = y − X b {\displaystyle {\hat {y}}=Xb,\quad e=y-{\hat {y}}=y-Xb} .

соответственно сумма квадратов остатков регрессии будет равна

R S S = e T e = (y − X b) T (y − X b) {\displaystyle RSS=e^{T}e=(y-Xb)^{T}(y-Xb)} .

Дифференцируя эту функцию по вектору параметров b {\displaystyle b} и приравняв производные к нулю, получим систему уравнений (в матричной форме):

(X T X) b = X T y {\displaystyle (X^{T}X)b=X^{T}y} .

В расшифрованной матричной форме эта система уравнений выглядит следующим образом:

(∑ x t 1 2 ∑ x t 1 x t 2 ∑ x t 1 x t 3 … ∑ x t 1 x t k ∑ x t 2 x t 1 ∑ x t 2 2 ∑ x t 2 x t 3 … ∑ x t 2 x t k ∑ x t 3 x t 1 ∑ x t 3 x t 2 ∑ x t 3 2 … ∑ x t 3 x t k ⋮ ⋮ ⋮ ⋱ ⋮ ∑ x t k x t 1 ∑ x t k x t 2 ∑ x t k x t 3 … ∑ x t k 2) (b 1 b 2 b 3 ⋮ b k) = (∑ x t 1 y t ∑ x t 2 y t ∑ x t 3 y t ⋮ ∑ x t k y t) , {\displaystyle {\begin{pmatrix}\sum x_{t1}^{2}&\sum x_{t1}x_{t2}&\sum x_{t1}x_{t3}&\ldots &\sum x_{t1}x_{tk}\\\sum x_{t2}x_{t1}&\sum x_{t2}^{2}&\sum x_{t2}x_{t3}&\ldots &\sum x_{t2}x_{tk}\\\sum x_{t3}x_{t1}&\sum x_{t3}x_{t2}&\sum x_{t3}^{2}&\ldots &\sum x_{t3}x_{tk}\\\vdots &\vdots &\vdots &\ddots &\vdots \\\sum x_{tk}x_{t1}&\sum x_{tk}x_{t2}&\sum x_{tk}x_{t3}&\ldots &\sum x_{tk}^{2}\\\end{pmatrix}}{\begin{pmatrix}b_{1}\\b_{2}\\b_{3}\\\vdots \\b_{k}\\\end{pmatrix}}={\begin{pmatrix}\sum x_{t1}y_{t}\\\sum x_{t2}y_{t}\\\sum x_{t3}y_{t}\\\vdots \\\sum x_{tk}y_{t}\\\end{pmatrix}},} где все суммы берутся по всем допустимым значениям t {\displaystyle t} .

Если в модель включена константа (как обычно), то x t 1 = 1 {\displaystyle x_{t1}=1} при всех t {\displaystyle t} , поэтому в левом верхнем углу матрицы системы уравнений находится количество наблюдений n {\displaystyle n} , а в остальных элементах первой строки и первого столбца - просто суммы значений переменных: ∑ x t j {\displaystyle \sum x_{tj}} и первый элемент правой части системы - ∑ y t {\displaystyle \sum y_{t}} .

Решение этой системы уравнений и дает общую формулу МНК-оценок для линейной модели:

b ^ O L S = (X T X) − 1 X T y = (1 n X T X) − 1 1 n X T y = V x − 1 C x y {\displaystyle {\hat {b}}_{OLS}=(X^{T}X)^{-1}X^{T}y=\left({\frac {1}{n}}X^{T}X\right)^{-1}{\frac {1}{n}}X^{T}y=V_{x}^{-1}C_{xy}} .

Для аналитических целей оказывается полезным последнее представление этой формулы (в системе уравнений при делении на n, вместо сумм фигурируют средние арифметические). Если в регрессионной модели данные центрированы , то в этом представлении первая матрица имеет смысл выборочной ковариационной матрицы факторов, а вторая - вектор ковариаций факторов с зависимой переменной. Если кроме того данные ещё и нормированы на СКО (то есть в конечном итоге стандартизированы ), то первая матрица имеет смысл выборочной корреляционной матрицы факторов, второй вектор - вектора выборочных корреляций факторов с зависимой переменной.

Немаловажное свойство МНК-оценок для моделей с константой - линия построенной регрессии проходит через центр тяжести выборочных данных, то есть выполняется равенство:

y ¯ = b 1 ^ + ∑ j = 2 k b ^ j x ¯ j {\displaystyle {\bar {y}}={\hat {b_{1}}}+\sum _{j=2}^{k}{\hat {b}}_{j}{\bar {x}}_{j}} .

В частности, в крайнем случае, когда единственным регрессором является константа, получаем, что МНК-оценка единственного параметра (собственно константы) равна среднему значению объясняемой переменной. То есть среднее арифметическое, известное своими хорошими свойствами из законов больших чисел, также является МНК-оценкой - удовлетворяет критерию минимума суммы квадратов отклонений от неё.

Простейшие частные случаи

В случае парной линейной регрессии y t = a + b x t + ε t {\displaystyle y_{t}=a+bx_{t}+\varepsilon _{t}} , когда оценивается линейная зависимость одной переменной от другой, формулы расчета упрощаются (можно обойтись без матричной алгебры). Система уравнений имеет вид:

(1 x ¯ x ¯ x 2 ¯) (a b) = (y ¯ x y ¯) {\displaystyle {\begin{pmatrix}1&{\bar {x}}\\{\bar {x}}&{\bar {x^{2}}}\\\end{pmatrix}}{\begin{pmatrix}a\\b\\\end{pmatrix}}={\begin{pmatrix}{\bar {y}}\\{\overline {xy}}\\\end{pmatrix}}} .

Отсюда несложно найти оценки коэффициентов:

{ b ^ = Cov ⁡ (x , y) Var ⁡ (x) = x y ¯ − x ¯ y ¯ x 2 ¯ − x ¯ 2 , a ^ = y ¯ − b x ¯ . {\displaystyle {\begin{cases}{\hat {b}}={\frac {\mathop {\textrm {Cov}} (x,y)}{\mathop {\textrm {Var}} (x)}}={\frac {{\overline {xy}}-{\bar {x}}{\bar {y}}}{{\overline {x^{2}}}-{\overline {x}}^{2}}},\\{\hat {a}}={\bar {y}}-b{\bar {x}}.\end{cases}}}

Несмотря на то что в общем случае модели с константой предпочтительней, в некоторых случаях из теоретических соображений известно, что константа a {\displaystyle a} должна быть равна нулю. Например, в физике зависимость между напряжением и силой тока имеет вид U = I ⋅ R {\displaystyle U=I\cdot R} ; замеряя напряжение и силу тока, необходимо оценить сопротивление. В таком случае речь идёт о модели y = b x {\displaystyle y=bx} . В этом случае вместо системы уравнений имеем единственное уравнение

(∑ x t 2) b = ∑ x t y t {\displaystyle \left(\sum x_{t}^{2}\right)b=\sum x_{t}y_{t}} .

Следовательно, формула оценки единственного коэффициента имеет вид

B ^ = ∑ t = 1 n x t y t ∑ t = 1 n x t 2 = x y ¯ x 2 ¯ {\displaystyle {\hat {b}}={\frac {\sum _{t=1}^{n}x_{t}y_{t}}{\sum _{t=1}^{n}x_{t}^{2}}}={\frac {\overline {xy}}{\overline {x^{2}}}}} .

Случай полиномиальной модели

Если данные аппроксимируются полиномиальной функцией регрессии одной переменной f (x) = b 0 + ∑ i = 1 k b i x i {\displaystyle f(x)=b_{0}+\sum \limits _{i=1}^{k}b_{i}x^{i}} , то, воспринимая степени x i {\displaystyle x^{i}} как независимые факторы для каждого i {\displaystyle i} можно оценить параметры модели исходя из общей формулы оценки параметров линейной модели. Для этого в общую формулу достаточно учесть, что при такой интерпретации x t i x t j = x t i x t j = x t i + j {\displaystyle x_{ti}x_{tj}=x_{t}^{i}x_{t}^{j}=x_{t}^{i+j}} и x t j y t = x t j y t {\displaystyle x_{tj}y_{t}=x_{t}^{j}y_{t}} . Следовательно, матричные уравнения в данном случае примут вид:

(n ∑ n x t … ∑ n x t k ∑ n x t ∑ n x t 2 … ∑ n x t k + 1 ⋮ ⋮ ⋱ ⋮ ∑ n x t k ∑ n x t k + 1 … ∑ n x t 2 k) [ b 0 b 1 ⋮ b k ] = [ ∑ n y t ∑ n x t y t ⋮ ∑ n x t k y t ] . {\displaystyle {\begin{pmatrix}n&\sum \limits _{n}x_{t}&\ldots &\sum \limits _{n}x_{t}^{k}\\\sum \limits _{n}x_{t}&\sum \limits _{n}x_{t}^{2}&\ldots &\sum \limits _{n}x_{t}^{k+1}\\\vdots &\vdots &\ddots &\vdots \\\sum \limits _{n}x_{t}^{k}&\sum \limits _{n}x_{t}^{k+1}&\ldots &\sum \limits _{n}x_{t}^{2k}\end{pmatrix}}{\begin{bmatrix}b_{0}\\b_{1}\\\vdots \\b_{k}\end{bmatrix}}={\begin{bmatrix}\sum \limits _{n}y_{t}\\\sum \limits _{n}x_{t}y_{t}\\\vdots \\\sum \limits _{n}x_{t}^{k}y_{t}\end{bmatrix}}.}

Статистические свойства МНК-оценок

В первую очередь, отметим, что для линейных моделей МНК-оценки являются линейными оценками, как это следует из вышеприведённой формулы. Для несмещенности МНК-оценок необходимо и достаточно выполнения важнейшего условия регрессионного анализа : условное по факторам математическое ожидание случайной ошибки должно быть равно нулю. Данное условие, в частности, выполнено, если

1. математическое ожидание случайных ошибок равно нулю, и
2. факторы и случайные ошибки - независимые случайные величины .

Второе условие - условие экзогенности факторов - принципиальное. Если это свойство не выполнено, то можно считать, что практически любые оценки будут крайне неудовлетворительными: они не будут даже состоятельными (то есть даже очень большой объём данных не позволяет получить качественные оценки в этом случае). В классическом случае делается более сильное предположение о детерминированности факторов, в отличие от случайной ошибки, что автоматически означает выполнение условия экзогенности. В общем случае для состоятельности оценок достаточно выполнения условия экзогенности вместе со сходимостью матрицы V x {\displaystyle V_{x}} к некоторой невырожденной матрице при увеличении объёма выборки до бесконечности.

Для того, чтобы кроме состоятельности и несмещенности , оценки (обычного) МНК были ещё и эффективными (наилучшими в классе линейных несмещенных оценок) необходимо выполнение дополнительных свойств случайной ошибки:

Данные предположения можно сформулировать для ковариационной матрицы вектора случайных ошибок V (ε) = σ 2 I {\displaystyle V(\varepsilon)=\sigma ^{2}I} .

Линейная модель, удовлетворяющая таким условиям, называется классической . МНК-оценки для классической линейной регрессии являются несмещёнными , состоятельными и наиболее эффективными оценками в классе всех линейных несмещённых оценок (в англоязычной литературе иногда употребляют аббревиатуру BLUE (Best Linear Unbiased Estimator ) - наилучшая линейная несмещённая оценка; в отечественной литературе чаще приводится теорема Гаусса - Маркова). Как нетрудно показать, ковариационная матрица вектора оценок коэффициентов будет равна:

V (b ^ O L S) = σ 2 (X T X) − 1 {\displaystyle V({\hat {b}}_{OLS})=\sigma ^{2}(X^{T}X)^{-1}} .

Эффективность означает, что эта ковариационная матрица является «минимальной» (любая линейная комбинация коэффициентов, и в частности сами коэффициенты, имеют минимальную дисперсию), то есть в классе линейных несмещенных оценок оценки МНК-наилучшие. Диагональные элементы этой матрицы - дисперсии оценок коэффициентов - важные параметры качества полученных оценок. Однако рассчитать ковариационную матрицу невозможно, поскольку дисперсия случайных ошибок неизвестна. Можно доказать, что несмещённой и состоятельной (для классической линейной модели) оценкой дисперсии случайных ошибок является величина:

S 2 = R S S / (n − k) {\displaystyle s^{2}=RSS/(n-k)} .

Подставив данное значение в формулу для ковариационной матрицы и получим оценку ковариационной матрицы. Полученные оценки также являются несмещёнными и состоятельными . Важно также то, что оценка дисперсии ошибок (а значит и дисперсий коэффициентов) и оценки параметров модели являются независимыми случайными величинами, что позволяет получить тестовые статистики для проверки гипотез о коэффициентах модели.

Необходимо отметить, что если классические предположения не выполнены, МНК-оценки параметров не являются наиболее эффективными и, где W {\displaystyle W} - некоторая симметрическая положительно определенная весовая матрица. Обычный МНК является частным случаем данного подхода, когда весовая матрица пропорциональна единичной матрице. Как известно, для симметрических матриц (или операторов) существует разложение W = P T P {\displaystyle W=P^{T}P} . Следовательно, указанный функционал можно представить следующим образом e T P T P e = (P e) T P e = e ∗ T e ∗ {\displaystyle e^{T}P^{T}Pe=(Pe)^{T}Pe=e_{*}^{T}e_{*}} , то есть этот функционал можно представить как сумму квадратов некоторых преобразованных «остатков». Таким образом, можно выделить класс методов наименьших квадратов - LS-методы (Least Squares).

Доказано (теорема Айткена), что для обобщенной линейной регрессионной модели (в которой на ковариационную матрицу случайных ошибок не налагается никаких ограничений) наиболее эффективными (в классе линейных несмещенных оценок) являются оценки т. н. обобщенного МНК (ОМНК, GLS - Generalized Least Squares) - LS-метода с весовой матрицей, равной обратной ковариационной матрице случайных ошибок: W = V ε − 1 {\displaystyle W=V_{\varepsilon }^{-1}} .

Можно показать, что формула ОМНК-оценок параметров линейной модели имеет вид

B ^ G L S = (X T V − 1 X) − 1 X T V − 1 y {\displaystyle {\hat {b}}_{GLS}=(X^{T}V^{-1}X)^{-1}X^{T}V^{-1}y} .

Ковариационная матрица этих оценок соответственно будет равна

V (b ^ G L S) = (X T V − 1 X) − 1 {\displaystyle V({\hat {b}}_{GLS})=(X^{T}V^{-1}X)^{-1}} .

Фактически сущность ОМНК заключается в определенном (линейном) преобразовании (P) исходных данных и применении обычного МНК к преобразованным данным. Цель этого преобразования - для преобразованных данных случайные ошибки уже удовлетворяют классическим предположениям.

Взвешенный МНК

В случае диагональной весовой матрицы (а значит и ковариационной матрицы случайных ошибок) имеем так называемый взвешенный МНК (WLS - Weighted Least Squares). В данном случае минимизируется взвешенная сумма квадратов остатков модели, то есть каждое наблюдение получает «вес», обратно пропорциональный дисперсии случайной ошибки в данном наблюдении: e T W e = ∑ t = 1 n e t 2 σ t 2 {\displaystyle e^{T}We=\sum _{t=1}^{n}{\frac {e_{t}^{2}}{\sigma _{t}^{2}}}} . Фактически данные преобразуются взвешиванием наблюдений (делением на величину, пропорциональную предполагаемому стандартному отклонению случайных ошибок), а к взвешенным данным применяется обычный МНК.

ISBN 978-5-7749-0473-0 .

Эконометрика. Учебник / Под ред. Елисеевой И. И. - 2-е изд. - М. : Финансы и статистика, 2006. - 576 с. - ISBN 5-279-02786-3 .

Александрова Н. В. История математических терминов, понятий, обозначений: словарь-справочник. - 3-е изд.. - М. : ЛКИ, 2008. - 248 с. - ISBN 978-5-382-00839-4 . И.В Митин, Русаков В.С. Анализ и обработка экспериментальных данных- 5-е издание- 24с.

Находит широкое применение в эконометрике в виде четкой экономической интерпретации ее параметров.

Линейная регрессия сводится к нахождению уравнения вида

или

Уравнение вида позволяет по заданным значениям параметра х иметь теоретические значения результативного признака, подставляя в него фактические значения фактора х .

Построение линейной регрессии сводится к оценке ее параметров — а и в. Оценки параметров линейной регрессии могут быть найдены разными методами.

Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК).

МНК позволяет получить такие оценки параметров а и в, при которых сумма квадратов отклонений фактических значений ре-зультативного признака (у) от расчетных (теоретических) ми-нимальна:

Чтобы найти минимум функции, надо вычислить част-ные производные по каждому из параметров а и b и приравнять их к нулю.

Обозначим через S, тогда:

Преобразуя формулу, получим следующую систему нормальных уравнений для оценки параметров а и в :

Решая систему нормальных уравнений (3.5) либо методом последовательного исключения переменных, либо методом определителей, найдем искомые оценки параметров а и в.

Параметр в называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу.

Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции . Существуют разные модификации формулы линейного коэффициента корреляции. Некоторые из них приведены ниже:

Как известно, линейный коэффициент корреляции находится в границах: -1 ≤ ≤ 1.

Для оценки качества подбора линейной функции рассчитывается квадрат

Линейного коэффициента корреляции называемый коэффициентом детерминации . Коэффициент детерминации характеризует долю дисперсии результативного признака у, объясняемую регрессией, в общей дисперсии результативного признака:

Соответственно величина 1 - характеризует долю диспер-сии у, вызванную влиянием остальных не учтенных в модели факторов.

Вопросы для самоконтроля

1. Суть метода наименьших квадратов?

2. Сколькими переменными предоставляется парная регрессия?

3. Каким коэффициентом определяется теснота связи между переменами?

4. В каких пределах определяется коэффициент детерминации?

5. Оценка параметра b в корреляционно-регрессионном анализе?

1. Кристофер Доугерти. Введение в эконометрию. - М.: ИНФРА - М, 2001 - 402 с.

2. С.А. Бородич. Эконометрика. Минск ООО «Новое знание» 2001.

3. Р.У. Рахметова Краткий курс по эконометрике. Учебное пособие. Алматы. 2004. -78с.

4. И.И. Елисеева.Эконометрика. - М.: «Финансы и статистика»,2002

5. Ежемесячный информационно-аналитический журнал.

Нелинейные экономические модели. Нелинейные модели регрессии. Преобразование переменных.

Нелинейные экономические модели..

Преобразование переменных.

Коэффициент эластичности.

Если между экономическими явлениями существуют нели-нейные соотношения, то они выражаются с помощью соответ-ствующих нелинейных функций: например, равносторонней ги-перболы , параболы второй степени и д.р.

Различают два класса нелинейных регрессий:

1. Регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, например:

Полиномы различных степеней - , ;

Равносторонняя гипербола - ;

Полулогарифмическая функция - .

2. Регрессии, нелинейные по оцениваемым параметрам, например:

Степенная - ;

Показательная - ;

Экспоненциальная - .

Общая сумма квадратов отклонений индивидуальных значений результативного признака у от среднего значения вызвана влиянием множества причин. Условно разделим всю совокупность причин на две группы: изучаемый фактор х и прочие факторы.

Если фактор не оказывает влияния на результат, то линия регрес-сии на графике параллельна оси ох и

Тогда вся дисперсия результативного признака обусловлена воздействием прочих факторов и общая сумма квадратов отклонений совпадет с остаточной. Если же прочие факторы не влияют на результат, то у связан с х функционально и остаточная сумма квадратов равна нулю. В этом случае сумма квадратов отклонений, объясненная регрессией, совпадает с общей суммой квадратов.

Поскольку не все точки поля корреляции лежат на линии регрессии, то всегда имеет место их разброс как обусловленный вли-янием фактора х , т. е. регрессией у по х, так и вызванный действием прочих причин (необъясненная вариация). Пригод-ность линии регрессии для прогноза зависит от того, какая часть общей вариации признака у приходится на объясненную вариа-цию

Очевидно, что если сумма квадратов отклонений, обусловленная регрессией, будет больше остаточной суммы квадратов, то уравнение регрессии статистически значимо и фактор х оказывает существенное воздействие на результат у.

, т. е. с числом свободы независимого варьирования признака. Число степеней свободы связано с числом единиц совокупности n и с числом определяемых по ней констант. Применительно к исследуемой проблеме число степеней свободы должно показать, сколько независимых откло-нений из п

Оценка значимости уравнения регрессии в целом дается с по-мощью F -критерия Фишера. При этом выдвигается нулевая ги-потеза, что коэффициент регрессии равен нулю, т. е. b = 0, и следовательно, фактор х не оказывает влияния на результат у.

Непосредственному расчету F-критерия предшествует анализ дисперсии. Центральное место в нем занимает разложе-ние общей суммы квадратов отклонений переменной у от средне го значения у на две части - «объясненную» и «необъясненную»:

- общая сумма квадратов отклонений;

- сумма квадратов отклонения объясненная регрессией;

- остаточная сумма квадратов отклонения.

Любая сумма квадратов отклонений связана с числом степе-ней свободы, т. е. с числом свободы независимого варьирования признака. Число степеней свободы связано с числом единиц совокупности n и с числом определяемых по ней констант. Применительно к исследуемой проблеме число cтепеней свободы должно показать, сколько независимых откло-нений из п возможных требуется для образования данной суммы квадратов.

Дисперсия на одну степень свободы D .

F-отношения (F-критерий):

Ecли нулевая гипотеза справедлива , то факторная и остаточная дисперсии не отличаются друг от друга. Для Н 0 необходимо опровержение,чтобы факторная дисперсия превышала остаточную в несколько раз. Английским статистиком Снедекором раз-работаны таблицы критических значений F -отношений при разных уровняхсущественности нулевой гипотезы и различном числе степенейсвободы. Табличное значение F -критерия — это максимальная величина отношения дисперсий, которая может иметь место прислучайном их расхождении для данного уровня вероятности наличия нулевой гипотезы. Вычисленное значение F -отношения признается достоверным, если о больше табличного.

В этом случае нулевая гипотеза об отсутствии связи признаков отклоняется и делается вывод о существенности этой связи: F факт > F табл Н 0 отклоняется.

Если же величина окажется меньше табличной F факт ‹, F табл , то вероятность нулевой гипотезы выше заданного уровня и она не может быть отклонена без серьезного риска сделать неправильный вывод о наличии связи. В этом случае уравнение регрессии считается статистически незначимым. Н о не отклоняется.

Стандартная ошибка коэффициента регрессии

Для оценки существенности коэффициента регрессии его ве-личина сравнивается с его стандартной ошибкой, т. е. определяется фактическое значение t -критерия Стьюдентa: которое затем сравнивается с табличным значением при определенном уровне значимости и числе степеней свободы (n - 2).

Стандартная ошибка параметра а :

Значимость линейного коэффициента корреляции проверя-ется на основе величины ошибки коэффициента корреляции т r:

Общая дисперсия признака х :

Множественная линейная регрессия

Построение модели

Множественная регрессия представляет собой регрессию результативного признака с двумя и большим числом факторов, т. е. модель вида

Регрессия может дать хороший результат при модели-ровании, если влиянием других факторов, воздействующих на объект исследования, можно пренебречь. Поведение отдельных экономи-ческих переменных контролировать нельзя, т. е. не удается обес-печить равенство всех прочих условий для оценки влияния одно-го исследуемого фактора. В этом случае следует попытаться выявить влияние других факторов, введя их в модель, т. е. пост-роить уравнение множественной регрессии: y = a+b 1 x 1 +b 2 +…+b p x p + .

Основная цель множественной регрессии — построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также совокупное их воздействие на моделируемый показатель. Спецификация модели включает в себя два круга вопросов: отбор фак-торов и выбор вида уравнения регрессии

Пример.

Экспериментальные данные о значениях переменных х и у приведены в таблице.

В результате их выравнивания получена функция

Используя метод наименьших квадратов , аппроксимировать эти данные линейной зависимостью y=ax+b (найти параметры а и b ). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.

Суть метода наименьших квадратов (МНК).

Задача заключается в нахождении коэффициентов линейной зависимости, при которых функция двух переменных а и b принимает наименьшее значение. То есть, при данных а и b сумма квадратов отклонений экспериментальных данных от найденной прямой будет наименьшей. В этом вся суть метода наименьших квадратов.

Таким образом, решение примера сводится к нахождению экстремума функции двух переменных.

Вывод формул для нахождения коэффициентов.

Составляется и решается система из двух уравнений с двумя неизвестными. Находим частные производные функции по переменным а и b , приравниваем эти производные к нулю.

Решаем полученную систему уравнений любым методом (например методом подстановки или ) и получаем формулы для нахождения коэффициентов по методу наименьших квадратов (МНК).

При данных а и b функция принимает наименьшее значение. Доказательство этого факта приведено .

Вот и весь метод наименьших квадратов. Формула для нахождения параметра a содержит суммы , , , и параметр n - количество экспериментальных данных. Значения этих сумм рекомендуем вычислять отдельно. Коэффициент b находится после вычисления a .

Пришло время вспомнить про исходый пример.

Решение.

В нашем примере n=5 . Заполняем таблицу для удобства вычисления сумм, которые входят в формулы искомых коэффициентов.

Значения в четвертой строке таблицы получены умножением значений 2-ой строки на значения 3-ей строки для каждого номера i .

Значения в пятой строке таблицы получены возведением в квадрат значений 2-ой строки для каждого номера i .

Значения последнего столбца таблицы – это суммы значений по строкам.

Используем формулы метода наименьших квадратов для нахождения коэффициентов а и b . Подставляем в них соответствующие значения из последнего столбца таблицы:

Следовательно, y = 0.165x+2.184 - искомая аппроксимирующая прямая.

Осталось выяснить какая из линий y = 0.165x+2.184 или лучше аппроксимирует исходные данные, то есть произвести оценку методом наименьших квадратов.

Оценка погрешности метода наименьших квадратов.

Для этого требуется вычислить суммы квадратов отклонений исходных данных от этих линий и , меньшее значение соответствует линии, которая лучше в смысле метода наименьших квадратов аппроксимирует исходные данные.

Так как , то прямая y = 0.165x+2.184 лучше приближает исходные данные.

Графическая иллюстрация метода наименьших квадратов (мнк).

На графиках все прекрасно видно. Красная линия – это найденная прямая y = 0.165x+2.184 , синяя линия – это , розовые точки – это исходные данные.

Для чего это нужно, к чему все эти аппроксимации?

Я лично использую для решения задач сглаживания данных, задач интерполяции и экстраполяции (в исходном примере могли бы попросить найти занчение наблюдаемой величины y при x=3 или при x=6 по методу МНК). Но подробнее поговорим об этом позже в другом разделе сайта.

Доказательство.

Чтобы при найденных а и b функция принимала наименьшее значение, необходимо чтобы в этой точке матрица квадратичной формы дифференциала второго порядка для функции была положительно определенной. Покажем это.

КУРСОВАЯ РАБОТА

по дисциплине: Информатика

Тема: Аппроксимация функции методом наименьших квадратов

Введение

1. Постановка задачи

2. Расчётные формулы

Расчёт с помощью таблиц, выполненных средствами Microsoft Excel

Схема алгоритма

Расчет в программе MathCad

Результаты, полученные с помощью функции Линейн

Представление результатов в виде графиков

Введение

Целью курсовой работы является углубление знаний по информатике, развитие и закрепление навыков работы с табличным процессором Microsoft Excel и программным продуктом MathCAD и применение их для решения задач с помощью ЭВМ из предметной области, связанной с исследованиями.

Аппроксимация (от латинского "approximare" -"приближаться") - приближенное выражение каких-либо математических объектов (например, чисел или функций) через другие более простые, более удобные в пользовании или просто более известные. В научных исследованиях аппроксимация применяется для описания, анализа, обобщения и дальнейшего использования эмпирических результатов.

Как известно, между величинами может существовать точная (функциональная) связь, когда одному значению аргумента соответствует одно определенное значение, и менее точная (корреляционная) связь, когда одному конкретному значению аргумента соответствует приближенное значение или некоторое множество значений функции, в той или иной степени близких друг к другу. При ведении научных исследований, обработке результатов наблюдения или эксперимента обычно приходиться сталкиваться со вторым вариантом.

При изучении количественных зависимостей различных показателей, значения которых определяются эмпирически, как правило, имеется некоторая их вариабельность. Частично она задается неоднородностью самих изучаемых объектов неживой и, особенно, живой природы, частично - обуславливается погрешностью наблюдения и количественной обработке материалов. Последнюю составляющую не всегда удается исключить полностью, можно лишь минимизировать ее тщательным выбором адекватного метода исследования и аккуратностью работы. Поэтому при выполнении любой научно-исследовательской работы возникает проблема выявления подлинного характера зависимости изучаемых показателей, этой или иной степени замаскированных неучтенностью вариабельности: значений. Для этого и применяется аппроксимация - приближенное описание корреляционной зависимости переменных подходящим уравнением функциональной зависимости, передающим основную тенденцию зависимости (или ее "тренд").

При выборе аппроксимации следует исходить из конкретной задачи исследования. Обычно, чем более простое уравнение используется для аппроксимации, тем более приблизительно получаемое описание зависимости. Поэтому важно считывать, насколько существенны и чем обусловлены отклонения конкретных значений от получаемого тренда. При описании зависимости эмпирически определенных значений можно добиться и гораздо большей точности, используя какое-либо более сложное, много параметрическое уравнение. Однако нет никакого смысла стремиться с максимальной точностью передать случайные отклонения величин в конкретных рядах эмпирических данных. Гораздо важнее уловить общую закономерность, которая в данном случае наиболее логично и с приемлемой точностью выражается именно двухпараметрическим уравнением степенной функции. Таким образом, выбирая метод аппроксимации, исследователь всегда идет на компромисс: решает, в какой степени в данном случае целесообразно и уместно «пожертвовать» деталями и, соответственно, насколько обобщенно следует выразить зависимость сопоставляемых переменных. Наряду с выявлением закономерностей, замаскированных случайными отклонениями эмпирических данных от общей закономерности, аппроксимация позволяет также решать много других важных задач: формализовать найденную зависимость; найти неизвестные значения зависимой переменной путем интерполяции или, если это допустимо, экстраполяции.

В каждом задании формулируются условия задачи, исходные данные, форма выдачи результатов, указываются основные математические зависимости для решения задачи. В соответствии с методом решения задачи разрабатывается алгоритм решения, который представляется в графической форме.

1. Постановка задачи

1. Используя метод наименьших квадратов функцию , заданную таблично, аппроксимировать:

а) многочленом первой степени ;

б) многочленом второй степени ;

в) экспоненциальной зависимостью .

Для каждой зависимости вычислить коэффициент детерминированности.

Вычислить коэффициент корреляции (только в случае а).

Для каждой зависимости построить линию тренда.

Используя функцию ЛИНЕЙН вычислить числовые характеристики зависимости от .

Сравнить свои вычисления с результатами, полученными при помощи функции ЛИНЕЙН.

Сделать вывод, какая из полученных формул наилучшим образом аппроксимирует функцию .

Написать программу на одном из языков программирования и сравнить результаты счета с полученными выше.

Вариант 3. Функция задана табл. 1.

Таблица 1.

2. Расчётные формулы

Часто при анализе эмпирических данных возникает необходимость найти функциональную зависимость между величинами x и y, которые получены в результате опыта или измерений.

Хi (независимая величина) задается экспериментатором, а yi , называемая эмпирическими или опытными значениями получается в результате опыта.

Аналитический вид функциональной зависимости, существующей между величинами x и y обычно неизвестен, поэтому возникает практически важная задача - найти эмпирическую формулу

, (1)

(где - параметры), значения которой при возможно мало отличались бы от опытных значений.

Согласно методу наименьших квадратов наилучшими коэффициентами считаются те, для которых сумма квадратов отклонений найденной эмпирической функции от заданных значений функции будет минимальной.

Используя необходимое условие экстремума функции нескольких переменных - равенство нулю частных производных, находят набор коэффициентов , которые доставляют минимум функции, определяемой формулой (2) и получают нормальную систему для определения коэффициентов :

(3)

Таким образом, нахождение коэффициентов сводится к решению системы (3).

Вид системы (3) зависит от того, из какого класса эмпирических формул мы ищем зависимость (1). В случае линейной зависимости система (3) примет вид:

(4)

В случае квадратичной зависимости система (3) примет вид:

(5)

В ряде случаев в качестве эмпирической формулы берут функцию в которую неопределенные коэффициенты входят нелинейно. При этом иногда задачу удается линеаризовать т.е. свести к линейной. К числу таких зависимостей относится экспоненциальная зависимость

где a1и a2 неопределенные коэффициенты.

Линеаризация достигается путем логарифмирования равенства (6), после чего получаем соотношение

(7)

Обозначим и соответственно через и , тогда зависимость (6) может быть записана в виде , что позволяет применить формулы (4) с заменой a1 на и на .

График восстановленной функциональной зависимости y(x) по результатам измерений (xi, yi), i=1,2,…,n называется кривой регрессии. Для проверки согласия построенной кривой регрессии с результатами эксперимента обычно вводят следующие числовые характеристики: коэффициент корреляции (линейная зависимость), корреляционное отношение и коэффициент детерминированности.

Коэффициент корреляции является мерой линейной связи между зависимыми случайными величинами: он показывает, насколько хорошо в среднем может быть представлена одна из величин в виде линейной функции от другой.

Коэффициент корреляции вычисляется по формуле:

(8)

(9)

где - среднее арифметическое значение соответственно по x, y.

Коэффициент корреляции между случайными величинами по абсолютной величине не превосходит 1. Чем ближе к 1, тем теснее линейная связь между x и y.

В случае нелинейной корреляционной связи условные средние значения располагаются около кривой линии. В этом случае в качестве характеристики силы связи рекомендуется использовать корреляционное отношение, интерпретация которого не зависит от вида исследуемой зависимости.

Корреляционное отношение вычисляется по формуле:

(10)

где а числитель характеризует рассеяние условных средних около безусловного среднего.

Всегда. Равенство = соответствует случайным некоррелированным величинам; = тогда и только тогда, когда имеется точная функциональная связь между x и y. В случае линейной зависимости y от x корреляционное отношение совпадает с квадратом коэффициента корреляции. Величина используется в качестве индикатора отклонения регрессии от линейной.

Корреляционное отношение является мерой корреляционной связи y c x в какой угодно форме, но не может дать представления о степени приближенности эмпирических данных к специальной форме. Чтобы выяснить насколько точно построен5ная кривая отражает эмпирические данные вводится еще одна характеристика - коэффициент детерминированности.

Коэффициент детерминированности определяется по формуле:

где Sост = - остаточная сумма квадратов, характеризующая отклонение экспериментальных данных от теоретических.полн - полная сумма квадратов, где среднее значение yi.

- регрессионная сумма квадратов, характеризующая разброс данных.

Чем меньше остаточная сумма квадратов по сравнению с общей суммой квадратов, тем больше значение коэффициента детерминированности r2, который показывает, насколько хорошо уравнение, полученное с помощью регрессионного анализа, объясняет взаимосвязи между переменными. Если он равен 1, то имеет место полная корреляция с моделью, т.е. нет различия между фактическим и оценочным значениями y. В противоположном случае, если коэффициент детерминированности равен 0, то уравнение регрессии неудачно для предсказания значений y.

Коэффициент детерминированности всегда не превосходит корреляционное отношение. В случае когда выполняется равенство то можно считать, что построенная эмпирическая формула наиболее точно отражает эмпирические данные.

3. Расчёт с помощью таблиц, выполненных средствами Microsoft Excel

Для проведения расчётов данные целесообразно расположить в виде таблицы 2, используя средства табличного процессора Microsoft Excel.

Таблица 2

Поясним, как таблица 2 составляется.

Шаг 1.В ячейки А1:A25 заносим значения xi.

Шаг 2.В ячейки B1:B25 заносим значения уi.

Шаг 3.В ячейку С1 вводим формулу=А1^2.

Шаг 4.В ячейки С1:С25 эта формула копируется.

Шаг 5.В ячейку D1 вводим формулу=А1*B1.

Шаг 6.В ячейки D1:D25 эта формула копируется.

Шаг 7.В ячейку F1 вводим формулу=А1^4.

Шаг 8.В ячейки F1:F25 эта формула копируется.

Шаг 9.В ячейку G1 вводим формулу=А1^2*B1.

Шаг 10.В ячейки G1:G25 эта формула копируется.

Шаг 11.В ячейку H1 вводим формулу = LN(B1).

Шаг 12.В ячейки H1:H25 эта формула копируется.

Шаг 13.В ячейку I1 вводим формулу=А1*LN(B1).

Шаг 14.В ячейки I1:I25 эта формула копируется.

Последующие шаги делаем с помощью автосуммирования S.

Шаг 15. В ячейку А26 вводим формулу = СУММ(А1:А25).

Шаг 16. В ячейку В26 вводим формулу = СУММ(В1:В25).

Шаг 17. В ячейку С26 вводим формулу = СУММ(С1:С25).

Шаг 18. В ячейку D26 вводим формулу = СУММ(D1:D25).

Шаг 19. В ячейку E26 вводим формулу = СУММ(E1:E25).

Шаг 20. В ячейку F26 вводим формулу = СУММ(F1:F25).

Шаг 21. В ячейку G26 вводим формулу = СУММ(G1:G25).

Шаг 22. В ячейку H26 вводим формулу = СУММ(H1:H25).

Шаг 23. В ячейку I26 вводим формулу = СУММ(I1:I25).

Аппроксимируем функцию линейной функцией . Для определения коэффициентов и воспользуемся системой (4). Используя итоговые суммы таблицы 2, расположенные в ячейках A26, B26, C26 и D26, запишем систему (4) в виде

(11)

решив которую, получим и .

Систему решали методом Крамера. Суть которого состоит в следующем. Рассмотрим систему n алгебраических линейных уравнений с n неизвестными:

(12)

Определителем системы называется определитель матрицы системы:

(13)

Обозначим - определитель, который получится из определителя системы Δ заменой j-го столбца на столбец

Таким образом, линейная аппроксимация имеет вид

Решение системы (11) проводим, пользуясь средствами Microsoft Excel. Результаты представлены в таблице 3.

Таблица 3

	Обратная матрица

В таблице 3 в ячейках A32:B33 записана формула {=МОБР(А28:В29)}.

В ячейках Е32:Е33 записана формула {=МУМНОЖ(А32:В33),(C28:С29)}.

Далее аппроксимируем функцию квадратичной функцией . Для определения коэффициентов a1, a2 и a3 воспользуемся системой (5). Используя итоговые суммы таблицы 2, расположенные в ячейках A26, B26, C26 , D26, E26, F26, G26 запишем систему (5) в виде

(16)

решив которую, получим a1=10,663624, и

Таким образом, квадратичная аппроксимация имеет вид

Решение системы (16) проводим, пользуясь средствами Microsoft Excel. Результаты представлены в таблице 4.

Таблица 4

	Обратная матрица

В таблице 4 в ячейках А41:С43 записана формула {=МОБР(А36:С38)}.

В ячейках F41:F43 записана формула {=МУМНОЖ(А41:C43),(D36:D38)}.

Теперь аппроксимируем функцию экспоненциальной функцией . Для определения коэффициентов и прологарифмируем значения и, используя итоговые суммы таблицы 2, расположенные в ячейках A26, C26, H26 и I26, получим систему

(18)

Решив систему (18), получим и .

После потенцирования получим .

Таким образом, экспоненциальная аппроксимация имеет вид

Решение системы (18) проводим, пользуясь средствами Microsoft Excel. Результаты представлены в таблице 5.

Таблица 5

	Обратная матрица

В ячейках А50:В51 записана формула {=МОБР(А46:В47)}.

В ячейках Е49:Е50 записана формула {=МУМНОЖ(А50:В51),(С46:С47)}.

В ячейке Е51 записана формула=EXP(E49).

Вычислим среднее арифметическое и по формулам:

Результаты расчета и средствами Microsoft Excel представлены в таблице 6.

Таблица 6

В ячейке В54 записана формула=А26/25.

В ячейке В55 записана формула=В26/25

Таблица 7

							Шаг 1.В ячейку J1 вводим формулу = (А1-$B$54)*(B1-$B$55). Шаг 2.В ячейки J2:J25 эта формула копируется. Шаг 3.В ячейку K1 вводим формулу = (А1-$B$54)^2. Шаг 4.В ячейки k2:K25 эта формула копируется. Шаг 5.В ячейку L1 вводим формулу = (B1-$B$55)^2. Шаг 6.В ячейки L2:L25 эта формула копируется. Шаг 7.В ячейку M1 вводим формулу = ($E$32+$E$33*A1-B1)^2. Шаг 8.В ячейки M2:M25 эта формула копируется. Шаг 9.В ячейку N1 вводим формулу = ($F$41+$F$42*A1+$F$43*A1^2-B1)^2. Шаг 10.В ячейки N2:N25 эта формула копируется. Шаг 11.В ячейку O1 вводим формулу = ($E$51*EXP($E$50*A1)-B1)^2. Шаг 12.В ячейки O2:O25 эта формула копируется. Последующие шаги делаем с помощью авто суммирования S. Шаг 13.В ячейку J26 вводим формулу = CУММ(J1:J25). Шаг 14.В ячейку K26 вводим формулу = CУММ(K1:K25). Шаг 15.В ячейку L26 вводим формулу = CУММ(L1:L25). Шаг 16.В ячейку M26 вводим формулу = CУММ(M1:M25). Шаг 17.В ячейку N26 вводим формулу = CУММ(N1:N25). Шаг 18.В ячейку O26 вводим формулу = CУММ(O1:O25). Теперь проведем расчеты коэффициента корреляции по формуле (8) (только для линейной аппроксимации) и коэффициента детерминированности по формуле (10). Результаты расчетов средствами Microsoft Excel представлены в таблице 8. Таблица 8 Коэффициент корреляции Коэффициент детерминированности (линейная аппроксимация) Коэффициент детерминированности (квадратичная аппроксимация) Коэффициент детерминированности (экспоненциальная аппроксимация) В ячейке E57 записана формула=J26/(K26*L26)^(1/2). В ячейке E59 записана формула=1-M26/L26. В ячейке E61 записана формула=1-N26/L26. В ячейке E63 записана формула=1-O26/L26. Анализ результатов расчетов показывает, что квадратичная аппроксимация наилучшим образом описывает экспериментальные данные. Схема алгоритма Рис. 1. Схема алгоритма для программы расчёта. 5. Расчет в программе MathCad Линейная регрессия · line (x, y) - вектор из двух элементов (b, a) коэффициентов линейной регрессии b+ax; · x - вектор действительных данных аргумента; · y - вектор действительных данных значений того же размера. Рисунок 2. Полиномиальная регрессия означает приближение данных (х1, у1) полиномом k-й степени При k=i полином является прямой линией, при k=2 - параболой, при k=3 - кубической параболой и т.д. Как правило, на практике применяются k<5. · regress (x,y,k) - вектор коэффициентов для построения полиномиальной регрессии данных; · interp (s,x,y,t) - результат полиномиальной регрессии; · s=regress(x,y,k); · x - вектор действительных данных аргумента, элементы которого расположены в порядке возрастания; · y - вектор действительных данных значений того же размера; · k - степень полинома регрессии (целое положительное число); · t - значение аргумента полинома регрессии. Рисунок 3 Кроме рассмотренных, в Mathcad встроено еще несколько видов трехпараметрической регрессии, их реализация несколько отличается от приведенных выше вариантов регрессии тем, что для них, помимо массива данных, требуется задать некоторые начальные значения коэффициентов a, b, c. Используйте соответствующий вид регрессии, если хорошо представляете себе, какой зависимостью описывается ваш массив данных. Когда тип регрессии плохо отражает последовательность данных, то ее результат часто бывает неудовлетворительным и даже сильно различающимся в зависимости от выбора начальных значений. Каждая из функций выдает вектор уточненных параметров a, b, c. Результаты, полученные с помощью функции ЛИНЕЙН Рассмотрим назначение функции ЛИНЕЙН. Эта функция использует метод наименьших квадратов, чтобы вычислить прямую линию, которая наилучшим образом аппроксимирует имеющиеся данные. Функция возвращает массив, который описывает полученную прямую. Уравнение для прямой линии имеет следующий вид: M1x1 + m2x2 + ... + b или y = mx + b, алгоритм табличный microsoft программный где зависимое значение y является функцией независимого значения x. Значения m - это коэффициенты, соответствующие каждой независимой переменной x, а b - это постоянная. Заметим, что y, x и m могут быть векторами. Для получения результатов необходимо создать табличную формулу, которая будет занимать 5 строк и 2 столбца. Этот интервал может располагаться в произвольном месте на рабочем листе. В этот интервал требуется ввести функцию ЛИНЕЙН. В результате должны заполниться все ячейки интервала А65:В69 (как показано в таблице 9). Таблица 9. Поясним назначение некоторых величин, расположенных в таблице 9. Величины, расположенные в ячейках А65 и В65 характеризуют соответственно наклон и сдвиг.- коэффициент детерминированности.- F-наблюдаемое значение.- число степеней свободы.- регрессионная сумма квадратов.- остаточная сумма квадратов. Представление результатов в виде графиков Рис. 4. График линейной аппроксимации Рис. 5. График квадратичной аппроксимации Рис. 6. График экспоненциальной аппроксимации Выводы Сделаем выводы по результатам полученных данных. Анализ результатов расчетов показывает, что квадратичная аппроксимация наилучшим образом описывает экспериментальные данные, т.к. линия тренда для неё наиболее точно отражает поведение функции на данном участке. Сравнивая результаты, полученные при помощи функции ЛИНЕЙН, видим, что они полностью совпадают с вычислениями, проведенными выше. Это указывает на то, что вычисления верны. Результаты, полученные с помощью программы MathCad, полностью совпадают со значениями приведенными выше. Это говорит о верности вычислений. Список используемой литературы 1 Б.П. Демидович, И.А. Марон. Основы вычислительной математики. М: Государственное издательство физико-математической литературы. 2 Информатика: Учебник под ред. проф. Н.В. Макаровой. М: Финансы и статистика, 2007. 3 Информатика: Практикум по технологии работы на компьютере под ред. проф. Н.В. Макаровой. М: Финансы и статистика, 2010. 4 В.Б. Комягин. Программирование в Excel на языке Visual Basic. М: Радио и связь, 2007. 5 Н. Николь, Р. Альбрехт. Excel. Электронные таблицы. М: Изд. «ЭКОМ», 2008. 6 Методические указания к выполнению курсовой работы по информатике (для студентов заочного отделения всех специальностей), под ред. Журова Г. Н., СПбГГИ(ТУ), 2011.

(см. рисунок). Требуется найти уравнение прямой

Чем меньше числа по абсолютной величине, тем лучше подобрана прямая (2). В качестве характеристики точности подбора прямой (2) можно принять сумму квадратов

Условия минимума S будут

	(6)
	(7)

Уравнения (6) и (7) можно записать в таком виде:

	(8)
	(9)

Из уравнений (8) и (9) легко найти a и b по опытным значениям x i и y i . Прямая (2), определяемая уравнениями (8) и (9), называется прямой, полученной по методу наименьших квадратов (этим названием подчеркивается то, что сумма квадратов S имеет минимум). Уравнения (8) и (9), из которых определяется прямая (2), называются нормальными уравнениями.

Можно указать простой и общий способ составления нормальных уравнений. Используя опытные точки (1) и уравнение (2), можно записать систему уравнений для a и b

y 1 =ax 1 +b,
y 2 =ax 2 +b, ...		(10)
y n =ax n +b,

Умножим левую и правую части каждого из этих уравнений на коэффициент при первой неизвестной a (т.е. на x 1 , x 2 , ..., x n) и сложим полученные уравнения, в результате получится первое нормальное уравнение (8).

Умножим левую и правую части каждого из этих уравнений на коэффициент при второй неизвестной b, т.е. на 1, и сложим полученные уравнения, в результате получится второе нормальное уравнение (9).

Этот способ получения нормальных уравнений является общим: он пригоден, например, и для функции

есть величина постоянная и ее нужно определить по опытным данным (1).

Систему уравнений для k можно записать:

Найти прямую (2) по методу наименьших квадратов.

Решение. Находим:

x i =21, y i =46,3, x i 2 =91, x i y i =179,1.

Записываем уравнения (8) и (9)

Отсюда находим

Оценка точности метода наименьших квадратов

Дадим оценку точности метода для линейного случая, когда имеет место уравнение (2).

Пусть опытные значения x i являются точными, а опытные значения y i имеют случайные ошибки с одинаковой дисперсией для всех i.

Введем обозначение

(16)

Тогда решения уравнений (8) и (9) можно представить в виде

	(17)
	(18)
где
	(19)
Из уравнения (17) находим
	(20)
Аналогично из уравнения (18) получаем
	(21)
так как
	(22)
Из уравнений (21) и (22) находим
	(23)

Уравнения (20) и (23) дают оценку точности коэффициентов, определенных по уравнениям (8) и (9).

Заметим, что коэффициенты a и b коррелированы. Путем простых преобразований находим их корреляционный момент.

Отсюда находим

0,072 при x=1 и 6,

0,041 при x=3,5.

Литература

Шор. Я. Б. Статистические методы анализа и контроля качества и надежности. М.:Госэнергоиздат, 1962, с. 552, С. 92-98.

Настоящая книга предназначается для широкого круга инженеров (научно-исследовательских институтов, конструкторских бюро, полигонов и заводов), занимающихся определением качества и надежности радиоэлектронной аппаратуры и других массовых изделий промышленности (машиностроения, приборостроения, артиллерийской и т.п.).

В книге дается приложение методов математической статистики к вопросам обработки и оценки результатов испытаний, при которых определяются качество и надежность испытываемых изделий. Для удобства читателей приводятся необходимые сведения из математической статистики, а также большое число вспомогательных математических таблиц, облегчающих проведение необходимых расчетов.

Изложение иллюстрируется большим числом примеров, взятых из области радиоэлектроники и артиллерийской техники.